A talk for parents about math at our school

Today, P led a session for the other parents at the school. We wanted to share the material and some links for those who weren't able to attend.

Agenda:

1. What does it mean to be good at math? What are we trying to achieve?
2. Key concepts we are using in teaching: Concrete-Pictorial-Abstract, Concept Progressions
3. Examples
4. What should parents do at home?

Good at Math

To start, P asked the parents, what does it mean to be good at math? Some of the answers:

• can add, subtract, multiply and divide
• calculate quickly
• able to estimate 

The range of opinions was good to see. Many ideas fell within the traditional answer: being good at math means being able to calculate precisely and quickly. We were especially pleased to hear skill at estimating as one of the ideas.

Our additions:

• Thinking logically. For example, if a certain thing is true, what else is true? 
• Looking for patterns and relationships; forming connections with other things they know.
• Asking questions about what they see, especially investigating structure
• Persevering

Admittedly, these are necessary for many other subjects. Math is a particularly good place to develop these skills because there is much greater objectivity and right/wrong are often clearly distinct. In this domain, the power of reasoning and independent thought is stronger than the power of authority.

Process of Learning Math

For this discussion, we focus on two key concepts in the way we teach and study math: (a) the Concrete-Pictorial-Abstract modes and (b) multiple models in progression and contrast.

C-P-A

"Concrete" means using physical objects. For example, a pile of 15 beads can be a concrete representation of the number 15. Taking 2 beads in the left hand and 3 in the right hand, then combining them is a concrete experience of adding 2 and 3.

In this mode, children are able to see, touch, move, examine, smell, and hear mathematics.  

"Pictorial" shifts to pictures on the page or board. For example, a picture of a room showing a vase with 2 flowers and another vase with 3 flowers can lead us to identify 5 flowers all together.

In this mode, children are able to see, construct (by drawing themselves), obliterate (by crossing out), and add color (by coloring, naturally) the mathematical objects.

"Abstract" is where we shift to symbols. For example, 2 + 3 = 5. This is a sequence of 5 symbols that don't offer any clues to their own meaning.  

In this mode, children are able to imagine and to move beyond physical constraints or necessities.

When new concepts are introduced, they generally go through each stage, starting with concrete, then pictorial, then abstract. This doesn't mean that abstract is superior, however. The ability to move back and forth, to give specific examples, to draw diagrams, to demonstrate a concrete model is also very important.

Multiple Models

Complementing the three modes, we also try to have multiple models, different ways of seeing, new concepts. There are two great resources that nicely illustrate this.  First, the models of multiplication posters from Natural Math:

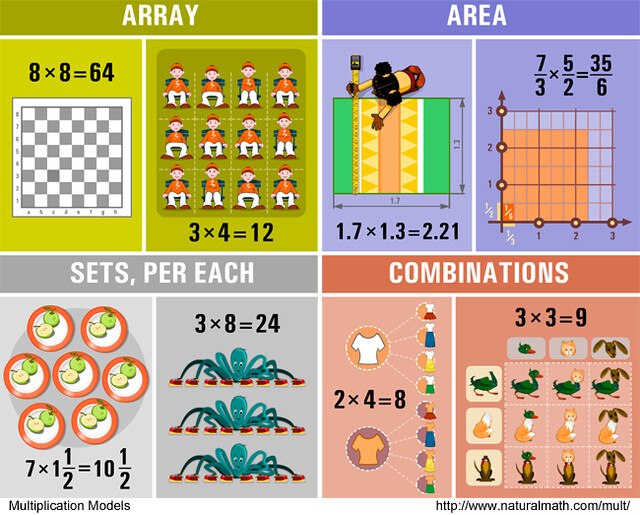4 of 12 models at Natural Maths

For the discussion, P gave examples of the equal groups model (sets per each), repeated addition, array, number line, and area.

I strongly encourage you to take a look at all 12 models in their poster, so here's the link again:
http://naturalmath.com/2013/09/12-models-of-multiplication/

The second resource is Graham Fletcher's series of progressions videos: Addition and Subtraction,
Multiplication, and Division.

For this talk, we presented abridged versions of the content in the multiplication and division videos. For your ease and viewing pleasure, here they are.

and the division video:



What to do at home
1) Ask questions
Parents can relax about being the source of knowledge. Don't worry about "teaching" or having the right answer. Instead, develop habits to cue thinking and their use of problem solving strategies:

• How do you know?
• What pictures could help us?
• What do you notice? What do you wonder? This works especially well if the parent serves as scribe writing down the kids' ideas.

"How do you know?" does three things. First, it is one way to escape from the child's questions "is this right?" Remember, the power of reasoning is stronger than the power of authority. We want to reinforce this by side-stepping calls to authority.

Second, it is a cue to get them thinking about their own thought process, which aids learning.

Third, this opens a potential discussion about different ways to attack the problem. Comparing and contrasting multiple strategies is a powerful tool for deeper learning.

"What pictures could help us?" is a cue to move between the Concrete-Pictorial-Abstract modes. If available, go to Concrete by asking about objects or physical models that are related.

"Notice & wonder" is a deep topic. One key idea is that, by serving as the scribe, we parents demonstrate that we care about the ideas that the kids have, we know they can contribute to solving the problem. This also gets us listening and understanding their perspective.

Notice & Wonder also involves skills that the kids will strengthen with practice, starting with superficial or (mathematically) irrelevant ideas and eventually moving on to thoughts about patterns and structure.

 For more about notice and wonder, please take a look at Annie Fetter's talk, 

2) Talking numbers to develop number sense
Two examples of number sense. Say we bought 8 bags of snacks and each bag cost 17 baht:

• I know that the total cost is not 1000 baht based on understanding order of magnitude.
• I know that the total cost is not 137 baht based on the pattern that all multiples of 8 are even

Like learning a language, number sense takes practice, it requires frequent exposure, and is built up by drawing children's attention to numerical and mathematical ideas.

Specific activities to do at home include estimating and measuring (length, time, weight, volume, etc).

Make math a part of everyday life by asking questions about what you see around and asking them to find examples of the concepts they are currently learning.

3) Play games
We play a lot of games at school and ask the kids to play them at home with their parents as homework. The games don't go stale when we move on, parents can play old games again. Some games are very calculation heavy. These are great opportunities to flex the Concrete-Pictorial-Abstract muscles.

Other games (or explorations) are much more about strategy. These are a great place to practice the other questions, especially "what do you notice?" and "what do you wonder?"