Grades 1 and 2
Mobius loopsWe are splitting up games with other activities. This week, we are introducing several geometry explorations. First up are Mobius strip activities, nicely shown in this Matt Parker second favorite shape:
- cylindrical loop: using 2 colored pencils, draw a line along the center of the loop on the inside and the outside. We can see that there are two sides, no big surprise. Cut along one of the lines and the loop splits into two new loops
- Mobius strip: give the paper a twist. Now, draw along the middle of the paper and see that there is only one side. Now, cut along this line and see what happens. Repeat this, drawing another line along the center of the new strip. Do you have one side or two? Again, cut along the central line. What do you get?
- Two connected loops: tape two, untwisted loops, together in perpendicular directions. Now cut along the center lines of each loop. What do you get?
- Two connected Mobius strips: tape together two mobius strips and cut along their center lines. What results now? Did everyone get the same result?
- try these with more twists (as per Matt's video)
- keep cutting the center lines
- Connect a Mobius strip and an untwisted loop (half-way step between 3 and 4). Now, cut along the center lines. What happens?
- Inspired by the thinner and thinner loops, kids can explore ways to cut paper so that they get longer and longer strips or loops
Also, in the class, we only had time for the first two make-and-cuts, then demonstrated the two connected loops.
Punch (fold and cut)
All this cutting fits nicely with our second exploration: the punch activities from Joel David Hamkins' post punch, fold, and cut from Joel David Hamkins.
Grades 3 and 4
We started with the Shapes x Shapes puzzle from NRICH:We added a couple of extra questions to this challenge:
- Before completing the puzzle, which numbers do they think are excluded? Why?
- Make extra equations that allow us to include those missing numbers. Are they easier to incorporate using multiplication or addition equations? What about equations that combine multiplication and addition?
Observations:
Once again, this appears to be a very simple activity, but gave us a lot to talk about. In particular, it was very helpful for highlighting a lot of misconceptions and gaps in understanding. Examples:
- "identity" relationships were still unclear: 1 x n = n, 0 x n = 0
- Several students thought the first equation would be 4x4x4 = 12 (confusing multiplication and addition)
Division Dice move to Cards
For our core activity, we are extending the Division Dice game. This time, we use playing cards, A through 10, instead of dice rolls to generate the random components of their equations. In this case, the aces are wild and can be any number from 2 to 10. When they form a multi=digit number with a 10, the 10 counts as two digits. For example, 3, 5, 10 could form 105 ÷ 3.
For our core activity, we are extending the Division Dice game. This time, we use playing cards, A through 10, instead of dice rolls to generate the random components of their equations. In this case, the aces are wild and can be any number from 2 to 10. When they form a multi=digit number with a 10, the 10 counts as two digits. For example, 3, 5, 10 could form 105 ÷ 3.
With cards instead of dice, we lack the natural move of flipping the dice to the opposite side which we used to make sure all throws could give us whole number divisions. In this version, we allow division with remainder. However, the twist is that the remainder becomes points for the opponent.
For example, if I draw 3, 3, 5, I can form 53 ÷ 3 to score 17 points for myself, but the opponent gets 2 points.
Question: Are there cases where the best play is not to form the largest possible number divided by the smallest number?
An interesting game variant: swap the scoring so that the active player scores the remainder and their opponent scores the quotient.
For example, if I draw 3, 3, 5, I can form 53 ÷ 3 to score 17 points for myself, but the opponent gets 2 points.
Question: Are there cases where the best play is not to form the largest possible number divided by the smallest number?
An interesting game variant: swap the scoring so that the active player scores the remainder and their opponent scores the quotient.
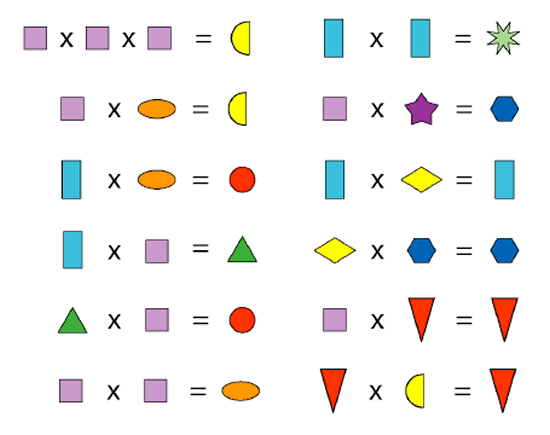
No comments:
Post a Comment